Resistencia de materiales - Método de Clebsch



La ecuación diferencial del eje de la viga deformada de la que partimos en Método de Clebscha tiene la siguiente forma:
\(E J \frac{d^2 y}{d x^2}=-M_g\)
El producto \(E J\) es una notación general de la rigidez a la flexión, donde:

- E - módulo de Young,
- J - momento de inercia de la sección de la viga respecto al eje horizontal.


El signo „-" a la derecha de la ecuación se debe al sistema de coordenadas adoptado
y al acuerdo que define el signo del momento flector.
Específicamente, la suposición de deflexiones positivas hacia abajo, y por lo tanto, la dirección positiva del eje de deflexión hacia abajo.

Para determinar las deflexiones de la viga, integramos dos veces la ecuación anterior
y obtenemos la primera derivada - la función del ángulo de rotación de la viga
\begin{gathered} \varphi=\frac{d y}{d x}=-\frac{1}{E J}\left(\int M_g d x+C\right) \\ \end{gathered}

y la segunda derivada - la función de deflexión
\begin{gathered} y=-\frac{1}{E J}\left(\int\left(\int M_g d x\right) d x+C x+D\right) \end{gathered}
donde:
C y D son constantes de integración.

Las constantes de integración se determinan a partir de las condiciones de contorno cinemáticas, es decir, condiciones sobre deflexiones nulas y ángulos de deflexión en un tipo específico de apoyo. Vea cuáles son los tipos de apoyos para una viga en el plano

Como hemos observado, el método de Clebscha, manteniendo ciertas condiciones de forma de escritura, permite para una viga simple obtener la ecuación de la línea de deflexión que contiene solo dos incógnitas (constantes de integración) independientemente del número de intervalos.

Las reglas que regulan el uso del método de Clebscha se pueden resumir en 4 puntos:

- los cortes en todos los intervalos deben medirse desde el mismo punto
asumimos para la viga simple un solo sistema de coordenadas, no podemos escribir, por ejemplo, parte de la función desde un lado y parte desde el otro lado de la viga

- en caso de que actúe una carga continua, no puede interrumpirse
si tal caso ocurre, la carga continua debe extenderse hasta el final de la viga, añadiendo al mismo tiempo una carga igual, con signo opuesto (contracarga)
- todos los nuevos términos que ingresen en la expresión del momento flector deben contener el factor \( (x- l_{i-1}) \),
donde:
\(l_{i-1}\) representa la coordenada del inicio del i-ésimo intervalo de la viga

- en caso de aparición de un momento concentrado M – multiplicamos el momento por el brazo de acción elevado a la potencia 0

\(M\cdot (x-l_{i-1})^0\),

- la integración debe realizarse sin desarrollar expresiones en paréntesis
las constantes de integración son válidas para toda la viga (para todos los intervalos)
Si las coordenadas \(l_{\mathrm{i}}\) determinan la posición de fuerzas concentradas \(P_{\mathrm{i}}\) o los inicios de la carga continua \(q_{\mathrm{i}}\), entonces expresiones del tipo \(P_i\left(x-l_i\right)\) o \(q_i \frac{\left(x-l_i\right)^2}{2}\) se integran según el esquema

\(\int\left(x-l_i\right)^n d x=\frac{\left(x-l_i\right)^{n+1}}{n+1}+C\)


De este curso aprenderás
Método de Clebscha (analítico):
- cómo determinar la función del momento para la viga en el método de Clebscha,
- cómo escribir la ecuación diferencial del eje deformado y cómo integrarla,
- cómo calcular las constantes de integración de la ecuación a partir de las condiciones de contorno para diferentes tipos de vigas,
- cómo calcular la deflexión y el ángulo de rotación en cualquier punto de la viga.

Sistemas estáticamente indeterminados:
- cómo determinar las reacciones en una viga estáticamente indeterminada mediante el método de Clebscha.

Y ahora, veamos el ejemplo a continuación y observemos la solución en la práctica.

Ver ejemplo

Viga de tres intervalos con diferentes tipos de cargas.
Calcular la deflexión y el ángulo de rotación en un punto dado de la viga.

Solución del ejemplo del video-curso

Contenido

Calcular la deflexión en el punto A.
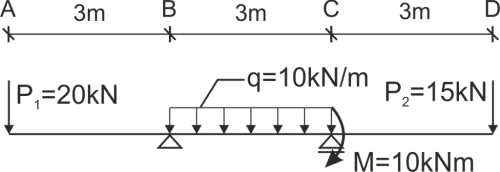
Ejemplo 1-método Clebscha

Solución

Calculamos las reacciones de apoyo

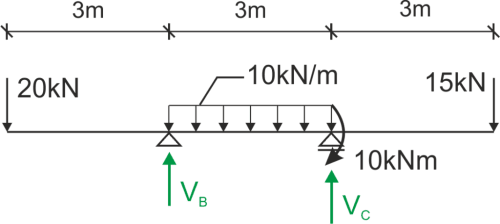\begin{aligned} &\sum{M_B}=0 -20\cdot 3+30\cdot 1.5+10+15\cdot 6-R_C\cdot 3=0 R_A=28.33kN\\ &\sum{M_C}=0 -20\cdot 6+R_B\cdot 3-30\cdot 1.5+10+15\cdot 3=0 R_B=36.67kN\\ &\sum{P_iY}=0 -20+R_B-30+R_C-15=0 L=P\\ \end{aligned}

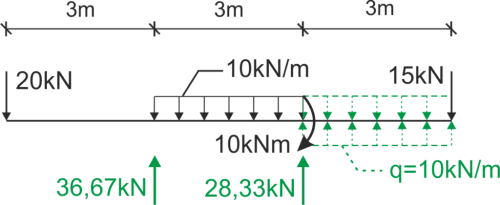
Escribimos la función del momento desde el lado izquierdo.

La función también se puede escribir desde el lado derecho. Te animamos a verificar esta variante, calcular el desplazamiento buscado y comparar los resultados.

\begin{aligned} &M_g(x)=-20x+R_B(x-3)-\frac{1}{2}q(x-3)^2+R_C(x-6)+10(x-6)^0+\frac{1}{2}q(x-6)^2\\ &EJ\cdot w"=-M_g(x)=20x-R_B(x-3)+5(x-3)^2- 28.33(x-6)-10(x-6)^0-5(x-6)^2\\ &EJ\cdot w'=20\frac{x^2}{2}-36.67\frac{(x-3)^2}{2}+5\frac{(x-3)^3}{3}-28.33\frac{(x-6)^2}{2}-10(x-6)-5\frac{(x-6)^3}{3}+C\\ &EJ\cdot w=20\frac{x^3}{6}-36.67\frac{(x-3)^3}{6}+5\frac{(x-3)^4}{12}-28.33\frac{(x-6)^3}{6}-10\frac{(x-6)^2}{2}-5\frac{(x-6)^4}{12}+Cx+D\\ \end{aligned}

Condiciones de contorno

\begin{aligned} &w(x=3)=0 \Rightarrow 90+3C+D=0\\ &w(x=6)=0 \Rightarrow 588.735+6C+D=0\\ &C=-166,245\\ &D=408.735\\ \end{aligned}

Calculamos la deflexión en el punto A.

Si hemos asumido el sistema de coordenadas en el extremo izquierdo de la viga, entonces el punto A tiene la coordenada x=0.

Por lo tanto \begin{aligned} &w_A(x=0)=\frac{1}{EI}\cdot (D)\\ \end{aligned} \begin{aligned} &w_A=\frac{1}{EI}\cdot (408.735)\\ \end{aligned}